Maurice Weiler @maurice_weiler
AI researcher with a focus on geometric DL and equivariant CNNs. PhD with Max Welling. Master's degree in physics. maurice-weiler.gitlab.io Amsterdam, The Netherlands Joined January 2018-
Tweets693
-
Followers3K
-
Following987
-
Likes1K
After two good years at Microsoft Research AI4Science, I am very excited to announce that as of this month I have, together with Chad Edwards, co-founded a new startup in the field of molecular and materials discovery.
Our survey "Hyperbolic Deep Learning in Computer Vision: A Survey" has been accepted to #IJCV! The survey provides an organization of supervised and unsupervised hyperbolic literature. Online now: link.springer.com/article/10.100… w/ @GhadimiAtigMina @mkellerressel @jeffhygu @syeung10
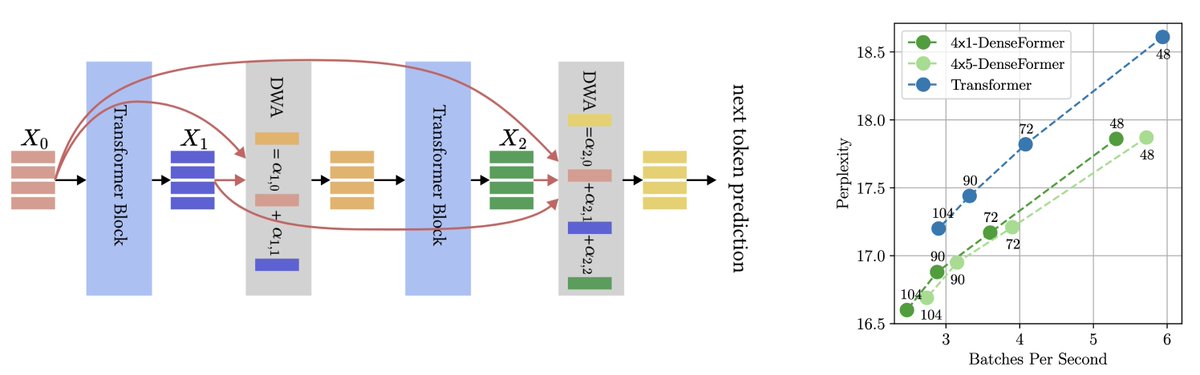
A tweak in the architecture of #Transformers can significantly boost accuracy! With direct access to all previous blocks’ outputs, a 48-block #DenseFormer outperforms a 72-block Transformer, with faster inference! A work with @akmohtashami_a,@francoisfleuret, Martin Jaggi. 1/🧵
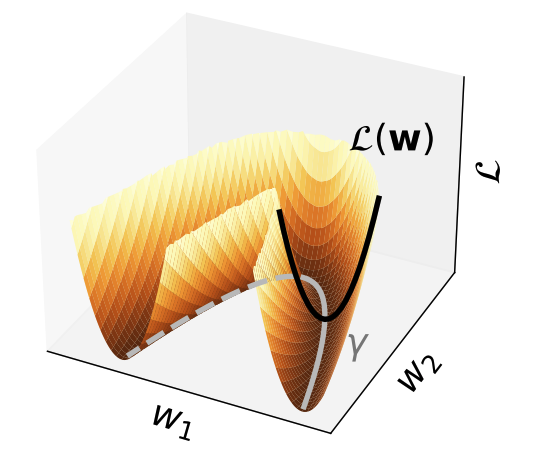
How does symmetry in #NeuralNetworks parameters impact learning? Check out our #ICLR2024 🔥spotlight🔥 paper on ``Improving Convergence and Generalization using Parameter Symmetries'' Paper: openreview.net/pdf?id=L0r0Gph… (1/3)
A thread of #gget threads - all gget updates in chronological order I will continue to add to this threadception as we post more updates. 🧵🧵 pachterlab.github.io/gget/
Our paper: “Clifford Group Equivariant Simplicial Message Passing Networks” has been accepted at #ICLR2024! With @djjruhe and @FEijkelboom, we explored the synergy of geometry and topology for better representations in geometric graphs! 📐 More details will come soon!
A new version of the Hitchhiker’s Guide is up, including general improvements: - a blurb on frame-based invariant GNNs (like AF2’s IPA) - new citations for unconstrained GNNs - clarifications on the universality of GemNet - and this hand-drawn figure PDF: arxiv.org/abs/2312.07511
Happy to share that our paper "Towards a transferable fermionic neural wavefunction for molecules", jointly with @MScherbela and @LeonGerard5 has finally appeard in Nature Communications @NatureComms see nature.com/articles/s4146…
The code for MOFDiff (accepted to ICLR 2024) is now open-sourced: github.com/microsoft/MOFD…
The code for MOFDiff (accepted to ICLR 2024) is now open-sourced: github.com/microsoft/MOFD…
Look what arrived! @maurice_weiler’s thesis (I’m on his thesis committee). Also basis of book with Patrick Forré, @erikverlinde and @wellingmax. maurice-weiler.gitlab.io/#cnn_book
"... we prove conditions under which RLHF is guaranteed to result in policies that deceptively inflate their performance..." Instead of aligning their policy, agents may evade by starting to lie or hide undesired behavior 🤥 Very interesting paper and well formalized results!
"... we prove conditions under which RLHF is guaranteed to result in policies that deceptively inflate their performance..." Instead of aligning their policy, agents may evade by starting to lie or hide undesired behavior 🤥 Very interesting paper and well formalized results!
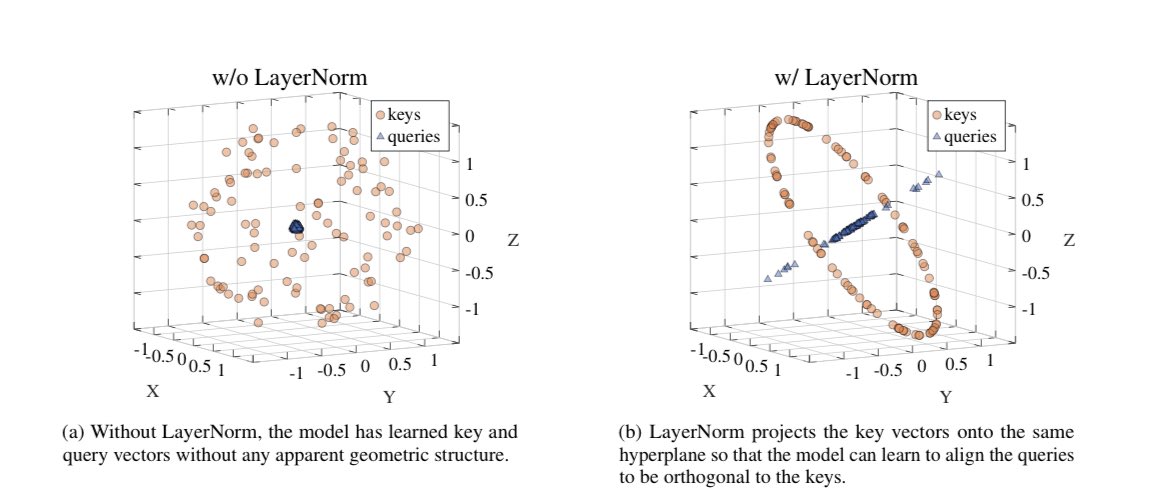
My two contenders: 1) Why LayerNorm is so helpful in Attention and what it’s actually doing under the hood (arxiv.org/abs/2305.02582) 2) Explaining the oversquashing phenomenon in GNNs (arxiv.org/abs/2006.05205) Really cool papers with superrr approachable math/theory 🙌🏻
My two contenders: 1) Why LayerNorm is so helpful in Attention and what it’s actually doing under the hood (arxiv.org/abs/2305.02582) 2) Explaining the oversquashing phenomenon in GNNs (arxiv.org/abs/2006.05205) Really cool papers with superrr approachable math/theory 🙌🏻 https://t.co/rAxJnDaDum
Read Yu Qing Xie & @tesssmidt on symmetry breaking and equivariant networks arxiv.org/abs/2402.02681
I am proud to present TopoX, a suite of packages that facilitate deep learning computations on topological spaces. Many thanks everyone who contributed to this effort @PyT_Team_ arxiv.org/pdf/2402.02441…
🚨New paper!🚨 Self-Rewarding LMs - LM itself provides its own rewards on own generations via LLM-as-a-Judge during Iterative DPO - Reward modeling ability improves during training rather than staying fixed ...opens the door to superhuman feedback? arxiv.org/abs/2401.10020 🧵(1/5)
Accepted at ICLR! github.com/ebekkers/ponita We derived pair-wise invariants that capture all geometric info needed to build simple + efficient SE(n) equivariant networks 🐴🔥 SOTA on 5 benchmarks (incl generation of molecules). Oh right, and ✨convolution is still all you need!

Michael Bronstein @mmbronstein
43K Followers 4K Following #DeepMind Professor of #AI @UniofOxford / Fellow @ExeterCollegeOx / ML Lead @ProjectCETI / https://t.co/kZpGpDzYeV
Sindy Löwe @sindy_loewe
3K Followers 361 Following PhD Student with @WellingMax at the University of Amsterdam. Deep Learning with Structured Representations.
Taco Cohen @TacoCohen
21K Followers 3K Following Deep learner at FAIR. Into codegen, equivariance, generative models. Spent time at Qualcomm, Scyfer (acquired), UvA, Deepmind, OpenAI.
Max Welling @wellingmax
32K Followers 429 Following
Frank Nielsen @FrnkNlsn
23K Followers 1K Following Machine Learning & AI, Information Sciences & Information Geometry, Distances & Statistical models, HPC. "Geometry defines the architecture of spaces" @SonyCSL
Frank Noe @FrankNoeBerlin
10K Followers 577 Following Scientist, #MachineLearning and #AI for the Sciences (esp. Physics/Chemistry). Scuba Diver and Traveler.
Kyle Cranmer @KyleCranmer
16K Followers 3K Following Director Data Science Institute @UWMadison @datascience_uw. EiC @MLSTjournal. Physics, stats/ML/AI, open science. same handle @sigmoid.social and bsky
Symmetry and Geometry.. @neur_reps
3K Followers 1K Following NeurIPS workshop and digital community | 🌐 geometry, algebra, topology + 🤖 deep learning + 🧠 neuroscience | Join us on slack! https://t.co/Run9wPnZt9
Hannes Stärk @HannesStaerk
8K Followers 332 Following @MIT PhD student • ML for molecular biology and flow generative models
Learning on Graphs Co.. @LogConference
7K Followers 749 Following LoG is a new annual research conference that covers areas broadly related to machine learning on graphs and geometry, with a special focus on review quality.
Johannes Brandstetter @jo_brandstetter
3K Followers 620 Following Ass. Prof / Group Lead @jkulinz, Head of Research - AI4Simulation NXAI. Former @MSFTResearch, @UvA_Amsterdam, @CERN, @tu_wien
Dan Roy @roydanroy
45K Followers 2K Following ML / AI researcher, emphasis on theory. Research Director and Canada CIFAR AI Chair, @VectorInst Professor, @UofT (Statistics/CS)
Gabriele Corso @GabriCorso
4K Followers 637 Following PhD student @MIT • Research on Generative Models and Geometric Deep Learning for Biophysics • BA @CambridgeUni • Former @TwitterResearch, @DEShawGroup and @IBM
Miles Cranmer @MilesCranmer
12K Followers 903 Following Assistant Prof @Cambridge_Uni, works on AI for the physical sciences. Previously: Flatiron, DeepMind, Princeton, McGill.
Sander Dieleman @sedielem
50K Followers 2K Following Research Scientist at Google DeepMind. I tweet about deep learning (research + software), music, generative models (personal account).
Shubhendu Trivedi @_onionesque
7K Followers 850 Following Cultivated Abandon. Twitter interests: Machine learning research, applied mathematics, mathematical miscellany, ML for Physics/Chemistry, books.
Andrew White @andrewwhite01
20K Followers 2K Following Head of Sci/cofounder @FutureHouseSF. Prof of chem eng @UofR (on sabbatical). Wrote textbook on deep learning in chemistry (https://t.co/WXOkMs9pkB).
Michael Galkin @michael_galkin
5K Followers 269 Following AI Research Scientist @Intel AI Lab. Prev: Postdoc @Mila_Quebec & McGill. GraphML, Knowledge Graphs, GNNs, NLP. Grandmaster of 80's music (according to Spotify)
Sam Power @sp_monte_carlo
17K Followers 7K Following Lecturer in Maths & Stats at Bristol. Interested in probabilistic + numerical computation, statistical modelling + inference. (he / him)
Cristian Bodnar @crisbodnar
5K Followers 2K Following Senior Researcher @MSFTResearch | Simulations, Geometric Deep Learning, AI4Science
KrystinaFairbank @KrystinaFa41836
3 Followers 660 Following
Carlee Adil @AdilCarl
88 Followers 5K Following
Slikir @slikir34104
0 Followers 50 Following
Kassidy Ligman @KassidyLig92400
93 Followers 5K Following
Yusuke Abe @AbeYusuke3
441 Followers 5K Following searching for new ideas on how to solve the unanswered questions for all mankind humanity freedom sci/tech/med #rust #quantum #AI intp-ubr-mensa-2e ∞ for ∞
Jaylee Bless @JaylBles
56 Followers 5K Following
Hope Hargett @HargetHo
80 Followers 5K Following
Julián Guiral @GuiralJA
75 Followers 968 Following I am a Neuropsychologist interested in Networks Neuroscience, Computational Neuroscience, Language Studies and Data Science.
Nadene Aspegren @NadeneA41300
80 Followers 5K Following
Alvera Destree @destr_alv
76 Followers 5K Following
April Alvardo @AlvaApr
54 Followers 5K Following
Gram Workshop @GRaM_workshop
29 Followers 154 Following Hi, I am the official account for the first edition of GRaM: Geometry-grounded Representation learning and generative Modeling Workshop at ICML2024
Per @Per062068834668
0 Followers 4 Following
Karlee Zidzik @zidzik92907
86 Followers 5K Following
Martin Funkquist @MartinFunkquist
93 Followers 509 Following PhD student @ Linköping University, working on AI with integrating natural language with acting and planning
Jesse Wiers @JWiers99
1 Followers 9 Following
Lida Kanari @LidaKanari
717 Followers 856 Following Topological Data Analysis and Computational Neuroscience. Group leader, Blue Brain Project, EPFL
五点三十四 @wdsss44
1 Followers 30 Following
Chenda 💎 @chendabunkasem
2K Followers 1K Following Founder of @eightcellinc - a research group. AI research circa 2018. Computer scientist weaving Bayesian mechanics, geometry, energy, & hardware.
ADITYA KABRA @adityakabra
286 Followers 1K Following I love science, entrepreneurship, and building things. This is my playground to run little experiments and share my ideas, projects, and learnings.
Kacey Chapel @ChapelKac
70 Followers 5K Following
Manyana Tiwari @Manyana72
1 Followers 36 Following
Liam Altarac @LiamAltarac
25 Followers 131 Following
Ankur Parikh @ank_parikh
3K Followers 3K Following Staff Research Scientist at Google DeepMind. Former adjunct assistant prof at @NYU_Courant. PhD at @mldcmu. ML for Bio/Chem (Prev. NLP). All opinions my own.
Jada Stoler @jada_stol
38 Followers 5K Following
Karuna @karunakc_
1 Followers 80 Following
Max @mk251098
14 Followers 223 Following research intern at KAUST in visual computing | ML master student at Aalto. | ❤️ hiking
Stephan Roche @StephanSroche
10K Followers 4K Following Physicist - ICREA Research Prof. @icreacommunity @icn2nano @_BIST @ls_quant #quantumtechnologies #quantumcomputing #TopologicalMatter #spintronics #graphene
Muhammed Shuaibi @mshuaibii
299 Followers 290 Following Research Engineer at FAIR, @AIatMeta @OpenCatalyst
Jenny Roy @JennyRoy25345
1 Followers 925 Following
Danika Bickes @DaniBicke
55 Followers 5K Following
AxonDAO @AxonDAO
16K Followers 5K Following Building the future of #DeSci 🌐 NVIDIA AI Inception | Official $AXGT token updates 👉 https://t.co/dHsKVUcmNH
Antonios Tragoudaras @TonyTragoudaras
15 Followers 86 Following Graduate Student - Artificial Intelligence @UvA_Amsterdam
Wouter Kool @wouter_kool
251 Followers 242 Following PhD in Machine Learning & Optimization from University of Amsterdam
Vicente Mendes @Vicente2621
23 Followers 241 Following MSc Physics EPFL / Popper / Artificial Intelligence and Causal Inference / JUNITEC / ⚽️
Yofo Diame @YDiame87519
330 Followers 4K Following
Pankaj Gupta @pankaj_ipynb
28 Followers 920 Following The English language can not fully capture the depth and complexity of my thoughts. So I'm incorporating Emoji into my speech to better express myself 😉.
Rubén Ballester @rballeba
1K Followers 510 Following I'm a PhD student in (topological) persistence theory and topological machine learning at Universitat de Barcelona.
Xindong Chen @Dabenmao3
85 Followers 1K Following Postdoc researcher at Tsinghua University. #CellDynamics #Biophysics #Protein-Protein Interactions #AppliedMathematics #Drug-AIGC!
Miklos Kralik @KralikMiklos
33 Followers 145 Following Neuroscience + computers + everything else...
AK @_akhaliq
309K Followers 3K Following AI research paper tweets, ML @Gradio (acq. by @HuggingFace 🤗) dm for promo follow on Hugging Face: https://t.co/q2Qoey80Gx
Michael Bronstein @mmbronstein
43K Followers 4K Following #DeepMind Professor of #AI @UniofOxford / Fellow @ExeterCollegeOx / ML Lead @ProjectCETI / https://t.co/kZpGpDzYeV
Sindy Löwe @sindy_loewe
3K Followers 361 Following PhD Student with @WellingMax at the University of Amsterdam. Deep Learning with Structured Representations.
Gabriel Peyré @gabrielpeyre
92K Followers 449 Following @CNRS researcher at @ENS_ULM. One tweet a day on computational mathematics.
Petar Veličković @PetarV_93
30K Followers 555 Following Staff Research Scientist @GoogleDeepMind | Affiliated Lecturer @Cambridge_Uni | Associate @clarehall_cam | GDL Scholar @ELLISforEurope. Monoids. 🇷🇸🇲🇪🇧🇦
Taco Cohen @TacoCohen
21K Followers 3K Following Deep learner at FAIR. Into codegen, equivariance, generative models. Spent time at Qualcomm, Scyfer (acquired), UvA, Deepmind, OpenAI.
Max Welling @wellingmax
32K Followers 429 Following
David Pfau @pfau
22K Followers 1K Following Knowledge manifests itself in radiant dreams that shimmer like the wild sun Views are my own pfau at sigmoid dot social on 🦣 https://t.co/xqtVHHVI17 on 🦋
Frank Nielsen @FrnkNlsn
23K Followers 1K Following Machine Learning & AI, Information Sciences & Information Geometry, Distances & Statistical models, HPC. "Geometry defines the architecture of spaces" @SonyCSL
Frank Noe @FrankNoeBerlin
10K Followers 577 Following Scientist, #MachineLearning and #AI for the Sciences (esp. Physics/Chemistry). Scuba Diver and Traveler.
Kyle Cranmer @KyleCranmer
16K Followers 3K Following Director Data Science Institute @UWMadison @datascience_uw. EiC @MLSTjournal. Physics, stats/ML/AI, open science. same handle @sigmoid.social and bsky
Symmetry and Geometry.. @neur_reps
3K Followers 1K Following NeurIPS workshop and digital community | 🌐 geometry, algebra, topology + 🤖 deep learning + 🧠 neuroscience | Join us on slack! https://t.co/Run9wPnZt9
Hannes Stärk @HannesStaerk
8K Followers 332 Following @MIT PhD student • ML for molecular biology and flow generative models
Michael Black @Michael_J_Black
58K Followers 641 Following Director, Max Planck Institute for Intelligent Systems (@MPI_IS). Chief Scientist @meshcapade. Building 3D digital humans using vision, graphics, and learning.
Learning on Graphs Co.. @LogConference
7K Followers 749 Following LoG is a new annual research conference that covers areas broadly related to machine learning on graphs and geometry, with a special focus on review quality.
Kevin Patrick Murphy @sirbayes
42K Followers 334 Following Research Scientist at Google Brain / Deepmind. Interested in Bayesian Machine Learning.
Johannes Brandstetter @jo_brandstetter
3K Followers 620 Following Ass. Prof / Group Lead @jkulinz, Head of Research - AI4Simulation NXAI. Former @MSFTResearch, @UvA_Amsterdam, @CERN, @tu_wien
Dan Roy @roydanroy
45K Followers 2K Following ML / AI researcher, emphasis on theory. Research Director and Canada CIFAR AI Chair, @VectorInst Professor, @UofT (Statistics/CS)
Gabriele Corso @GabriCorso
4K Followers 637 Following PhD student @MIT • Research on Generative Models and Geometric Deep Learning for Biophysics • BA @CambridgeUni • Former @TwitterResearch, @DEShawGroup and @IBM
Jürgen Schmidhuber @SchmidhuberAI
107K Followers 0 Following Invented principles of meta-learning (1987), GANs (1990), Transformers (1991), very deep learning (1991), etc. Our AI is used many billions of times every day.
Lida Kanari @LidaKanari
717 Followers 856 Following Topological Data Analysis and Computational Neuroscience. Group leader, Blue Brain Project, EPFL
Kevin K. Yang 楊凱�.. @KevinKaichuang
16K Followers 5K Following Senior Researcher in BioML @MSFTResearch (@MSRNE). He/him/他. 🇹🇼
Stephan Roche @StephanSroche
10K Followers 4K Following Physicist - ICREA Research Prof. @icreacommunity @icn2nano @_BIST @ls_quant #quantumtechnologies #quantumcomputing #TopologicalMatter #spintronics #graphene
Horace He @cHHillee
23K Followers 449 Following Working at the intersection of ML and Systems @ PyTorch "My learning style is Horace twitter threads" - @typedfemale
Wouter Kool @wouter_kool
251 Followers 242 Following PhD in Machine Learning & Optimization from University of Amsterdam
Lorenzo Giusti @lorgiusti
686 Followers 264 Following Geometric and Topological Deep Learning for particle physics @cern
Ginestra Bianconi @gin_bianconi
4K Followers 198 Following Mathematical physicists working on networks, statistical mechanics, topology, non-linear dynamics. Author of "Multilayer networks: Structure and Function" (OUP)
Rubén Ballester @rballeba
1K Followers 510 Following I'm a PhD student in (topological) persistence theory and topological machine learning at Universitat de Barcelona.
Claudio Battiloro @ClaBat9
501 Followers 246 Following Postdoctoral fellow @Harvard @Harvard_data | Topological Signal Processing ⋂ Deep Learning | Former Visiting @PennEngineers UPenn
Stefano Falletta @FallettaStefano
239 Followers 389 Following Postdoctoral Fellow @Harvard - Condensed Matter Physics, Electronic Structure, Machine Learning
Stanley H. Chan @stanley_h_chan
7K Followers 137 Following Professor | computational imaging | machine learning | Purdue ECE
Jacob Bamberger @jacobbamberger
98 Followers 477 Following Looking for topology where it shouldn’t be. PhD student @CompSciOxford. Interested in Geometric Deep Learning and Applied Topology
Robert M. Gower 🇺�.. @gowerrobert
1K Followers 305 Following Often found scribbling down math with intermittent bursts of bashing out code. Research Scientist @ FlatironInstitute.
Av @whispsofviolet
3K Followers 836 Following (Avanti Shrikumar). Stanford Comp Bio PhD ‘20, MIT BS ‘13. C-PTSD survivor. Moved to 🇦🇺. Blue checked cos running awareness campaigns.
Mustafa Suleyman @mustafasuleyman
131K Followers 535 Following CEO, Microsoft AI | Author: The Coming Wave | Past: Co-founder, @InflectionAI & @GoogleDeepMind
Laura Luebbert @NeuroLuebbert
2K Followers 1K Following Geneticist turned bioinformatician · PhD candidate @Caltech · Prev @UniLeiden · Author of #gget (the program not the coffee bar, unfortunately) · German-Catalan
Oumar Kaba @sekoumarkaba
426 Followers 468 Following Ph.D. Student at @Mila_Quebec / @mcgillu • ML, Physics, Math • Science Comms Enthusiast. Former intern @MSFTResearch AI4Science
Siba Smarak Panigrahi @sibasmarak
335 Followers 410 Following MSc in CS @mcgillu and @Mila_Quebec | UG in CSE @IITKgp | Prev. @ProseMsft @Adobe @USCViterbi @mitidss
Arnab @ArnabMondal96
580 Followers 413 Following Ph.D. candidate @mcgillu + @Mila_Quebec | @ServiceNowRSRCH | Undergrad @IITKgp | Formerly: @MSFTResearch @Apple @samsungresearch
Cong Liu @CongLiu202212
57 Followers 73 Following PhD student in Machine Learning @AmlabUva @ai4science_lab @UvA_Amsterdam
Floor Eijkelboom @FEijkelboom
218 Followers 142 Following PhD candidate @UvA_Amsterdam | deep learning for (quantum) physics 🦭
Philipp Marquetand @marquetand
2K Followers 2K Following From theoretical chemistry to machine learning (he/him)
Michael Scherbela @MScherbela
57 Followers 74 Following PhD student interested in Machine Learning and Physics
Kamyar Azizzadeneshel.. @Azizzadenesheli
3K Followers 1K Following #Sr Scientist @nvidia, exp-prof at @Purdue #MachineLearning, #ArtificialIntelligence #NeuralOperator #AI+#Science
Julius Berner @julberner
536 Followers 265 Following Postdoc @caltech | PhD @univienna | former research intern @MetaAI and @nvidia | bridging theory and practice in deep learning
Gitta Kutyniok @GittaKutyniok
2K Followers 231 Following Bavarian AI Chair for Mathematical Foundations of AI @LMU_Muenchen; Adjunct Professor for ML @UiTromso
Philipp Grohs @GrohsPhilipp
537 Followers 170 Following Full Professor of Mathematical Data Science at @univienna and group leader at @oeaw.
Nakul Rampal @RampalNakul
2K Followers 763 Following Current: BIDMaP Fellow @UCBerkeley Past: PhD student @Cambridge_Uni /Student & Researcher @UCBerkeley ML/AI, Molecular simulation & Porous Materials
Vitalii Kleshchevniko.. @vitaliikl
2K Followers 1K Following Researcher @bayraktar_lab @StatGenomics @teichlab @sangerinstitute | Physics & AI to study cells, cell circuits & brains 🧠 | #SingleCell+spatial | 🌍🇺🇦to🇬🇧
Peter Koo @pkoo562
1K Followers 676 Following Assistant Professor @CSHL, advancing deep learning for genomics
antisense. @razoralign
13K Followers 64 Following We do not know about death, because we never know about life. https://t.co/5L9IhaBKH5
Ming "Tommy" Tang @tangming2005
30K Followers 2K Following Director of computational biology. On my way to helping 1 million people learn bioinformatics. Educator, Biotech, single cell. Also talks about leadership.
Vincent Dutordoir @vdutor
1K Followers 649 Following Research Scientist @GoogleDeepMind (AI for Science). Previously: PhD @CambridgeMLG, @SecondmindLabs
Yair Schiff @SchiffYair
165 Followers 122 Following
Volodymyr Kuleshov �.. @volokuleshov
8K Followers 997 Following AI Researcher. Prof @Cornell & @Cornell_Tech. Co-Founder @afreshai. PhD @Stanford.
Tri Dao @tri_dao
18K Followers 364 Following Incoming Asst. Prof @PrincetonCS, Chief Scientist @togethercompute. Machine learning & systems.
Aaron Gokaslan @SkyLi0n
2K Followers 343 Following Creator of the OpenWebText and OpenGPT2. @PyTorch Core Reviewer. PhD Student at @Cornell (interning at @MosaicML) Previously at @FacebookAI and @BrownUniversity
Jean-Philippe Vert @jeanphi_vert
1K Followers 53 Following
John Martyn @JohnMMartyn
610 Followers 153 Following PhD student @MIT. Exploring quantum information, computational physics, and machine learning
Sara Hooker @sarahookr
39K Followers 7K Following I lead @CohereForAI. Formerly Research @Google Brain @GoogleDeepmind. ML Efficiency at scale, LLMs, @trustworthy_ml. Changing spaces where breakthroughs happen.
Guillem Simeon @guillemsimeon
304 Followers 358 Following (He/him) Physicist. PhD student, @UPFBarcelona. Geometric deep learning and AI for science. 🏳️🌈
Steven De Keninck @enkimute
433 Followers 229 Following
Julia Bauman @JuliaBauman2
8K Followers 456 Following PhD student at @Stanford Genetics in @LarsMSteinmetz lab | Prev @broadinstitute | Explaining cool biotech to the world here and @ 60_SecondScience on TikTok
Gianfranco Bertone @gfbertone
3K Followers 1K Following Prof. Theoretical Astroparticle Physics @GRAPPAInstitute | Father of 2 | Author | President @PremioCosmos
Prof. Paola Grosso @PaolaGrossoWork
368 Followers 153 Following Computer scientist at @UvA_Amsterdam. Scientific director @UvA_IvI. Member of the MNS research group (@MnsUva). h.
Bruno Neri @neribr
346 Followers 2K Following Technical Leader - Artificial Intelligence and Machine Learning Enthusiast - Senior Software Engineer @altenitaliaAfter two good years at Microsoft Research AI4Science, I am very excited to announce that as of this month I have, together with Chad Edwards, co-founded a new startup in the field of molecular and materials discovery.
@maxxxzdn @djjruhe @jo_brandstetter @CongLiu202212 Where’s the original Pytorch code? I’d be interested in seeing what the error is.
Excited to report that starting Apr, 1, 2025, I will no longer be accepting grad students & PDs in my lab. We will only accept AGI scientists. U can try reaching me at [email protected] but don't hold ur breath.
@miniapeur @Pseudomanifold @mmbronstein @crisbodnar @ninamiolane @gin_bianconi @naturecomputes @jo_brandstetter @HajijMustafa @rballeba @lorgiusti @ClaBat9 @hansmriess We should add @maurice_weiler for sure as well! And potentially many other more junior researchers :-)
Our survey "Hyperbolic Deep Learning in Computer Vision: A Survey" has been accepted to #IJCV! The survey provides an organization of supervised and unsupervised hyperbolic literature. Online now: link.springer.com/article/10.100… w/ @GhadimiAtigMina @mkellerressel @jeffhygu @syeung10
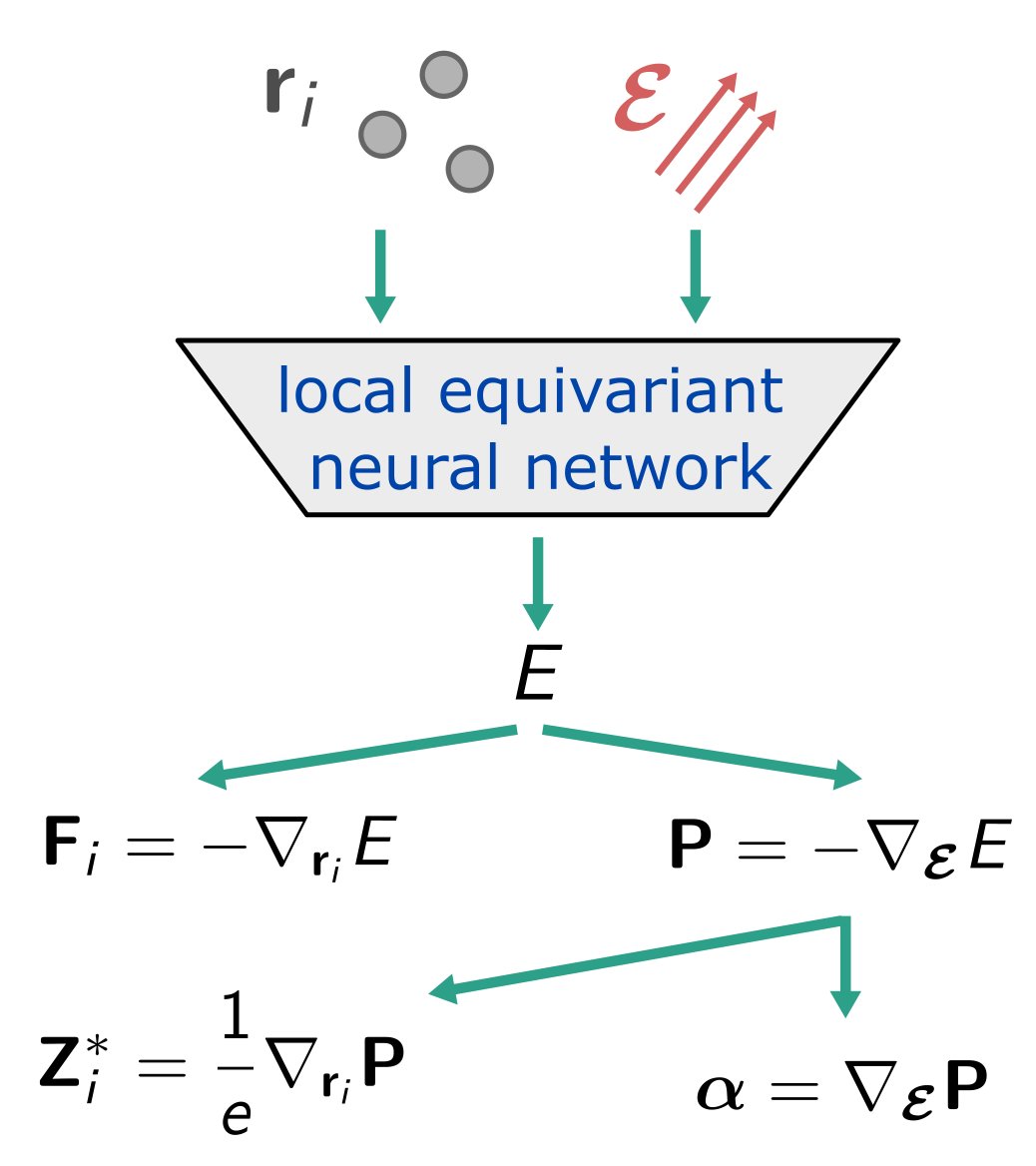
Happy to announce our Allegro model for unified learning of electric enthalpy, forces, polarization, Born charges, and polarizability through exact physical constraints. arxiv.org/abs/2403.17207 @bkoz37 @chuinwei_tan @ndrsjhnssn @cameron_cowen @Materials_Intel @hseas
TL;DR: Feed each layer of a transformer with a linear combination of the previous layers' outputs, and it works way better. And the learned coefficients have a cool structure (4th msg in the thread). With the awesome @MatPagliardini, @akmohtashami_a, and Martin Jaggi.
A tweak in the architecture of #Transformers can significantly boost accuracy! With direct access to all previous blocks’ outputs, a 48-block #DenseFormer outperforms a 72-block Transformer, with faster inference! A work with @akmohtashami_a,@francoisfleuret, Martin Jaggi. 1/🧵
A tweak in the architecture of #Transformers can significantly boost accuracy! With direct access to all previous blocks’ outputs, a 48-block #DenseFormer outperforms a 72-block Transformer, with faster inference! A work with @akmohtashami_a,@francoisfleuret, Martin Jaggi. 1/🧵
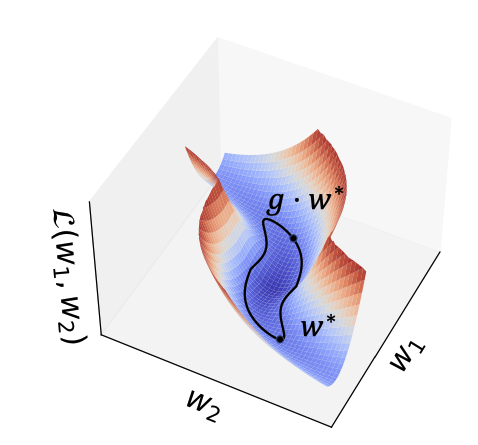
We also demonstrate the wide applicability of teleportation on various optimization tasks. This work was led by our amazing PhD student @BoZhao__ from @ucsd_cse, as a result of a great collaboration with @RobinSFWalters and @gowerrobert! (3/3)
We show that teleportation -- loss-invariant transformation in the parameter space -- not only accelerates optimization, but also improves generalization. We characterize such generalization behavior with the curvature of minima. (2/3)
How does symmetry in #NeuralNetworks parameters impact learning? Check out our #ICLR2024 🔥spotlight🔥 paper on ``Improving Convergence and Generalization using Parameter Symmetries'' Paper: openreview.net/pdf?id=L0r0Gph… (1/3)
@maurice_weiler @anshulkundaje @dmitrypenzar Ah, but if you dig that deep you also have to factor in how much extra compute is needed for an equivariant representation that achieves comparable performance to the "standard" models...if you try to match the number of parameters, you end up with equivariant models that have…
@maurice_weiler @anshulkundaje @dmitrypenzar @hannah_gzz Ok, I dug into the code, and...it turns @hannah_gzz did set it up correctly in the code (which I thought had to be the case since I recall verifying the models were RC equivariant). I just messed up the description. See below, the length axis (second axis) isn't flipped
@maurice_weiler @anshulkundaje @dmitrypenzar @hannah_gzz I must have gotten my wires crossed because of the flipping of the length axis before summing in the binary models, plus the ::-1 on the last axis (which in the case of the bias tracks refers to different smoothing levels on the input; this axis needs to be flipped due to how the…
@maurice_weiler @anshulkundaje @dmitrypenzar @hannah_gzz Will look into adding a note to correct the description. Thanks again for catching it!
@maurice_weiler @anshulkundaje @dmitrypenzar Hmm, with the caveat that the post hoc conjoined ensemble doesn't require an independent training run. So basically that ensemble is available "for free". In practice, you'd always opt for an ensemble that's available for free.
@maurice_weiler @anshulkundaje @dmitrypenzar @hannah_gzz I don't know if you have bandwidth to revisit these old experiments? There's a more principled way to handle the way we handled the bias strand in the RCPS models. No worries if not, I'm sure we can enlist a different summer intern if needed!
@maurice_weiler @anshulkundaje @dmitrypenzar Hmm, true re the RCPS weight sharing; if the output for the + strand ignores the flipped bias, the output on the - strand would have to ignore the "original orientation" bias. I think these sequences were centered (on chip seq signal peaks), which basically means I didn't expect…
@maurice_weiler @whispsofviolet @dmitrypenzar Looks like a fantastic book. Will try to read as I get some time.
.@NeuroLuebbert's gget now supports querying plant genomes. 🌱🌳🌵🌲🍃 github.com/pachterlab/gget